
ИКОНОМИЧЕСКИ
УНИВЕРСИТЕТ-ВАРНА
КУРСОВ ПРОЕКТ
по
ОПТИМИЗАЦИОННИ МЕТОДИ
Изготвил:
Проверил:
Александра Атанасова
Доц. др Б. Атанасов
Спец. Маркетинг гр 58 ф. №
9066
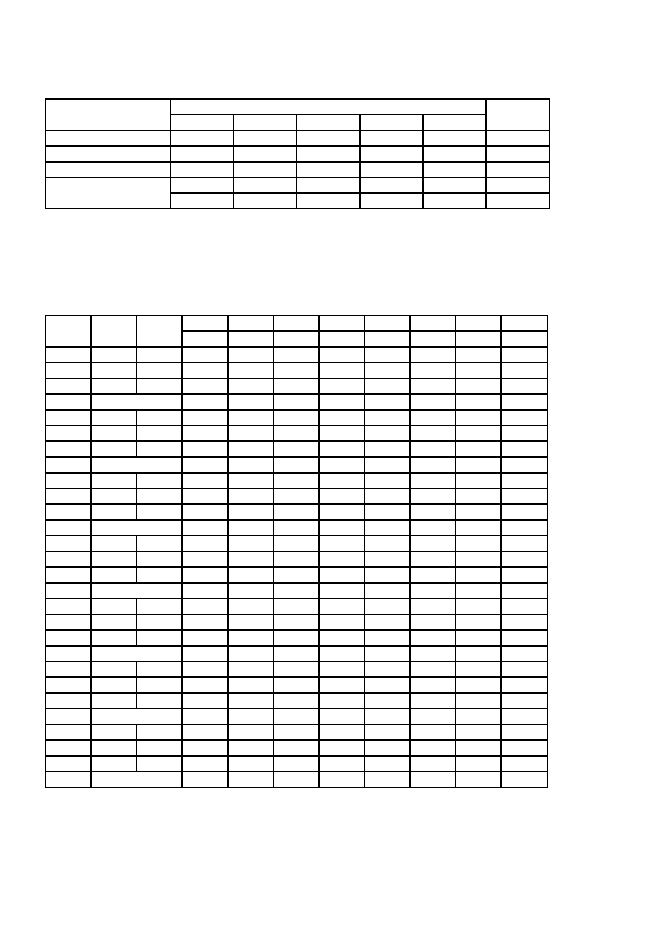
Видове ресурси
Разходни норми за едница продукция
Налични
ресурси
I
II
III
IV
V
A
6
3
3
3
3
1080
B
4
2
6
4
2
840
C
6
6
3
6
9
1440
Доход от единица
продукция
16
6
12
4
12
c
j
16
10
16
14
12
c
j
max:Z=16x
1
+10x
2
+16x
3
+14x
4
+12x
5
max:Z=16x
1
+10x
2
+16x
3
+14x
4
+12x
5
+0x
6
+0x
7
+0x
8
6x
1
+3x
2
+3x
3
+3x
4
+3x
5
≤1080 6x
1
+3x
2
+3x
3
+3x
4
+3x
5
+x
6
=1080
4x
1
+2x
2
+6x
3
+4x
4
+2x
5
≤840 4x
1
+2x
2
+6x
3
+4x
4
+2x
5
+x
7
= 840
6x
1
+6x
2
+3x
3
+6x
4
+9x
5
≤1440 6x
1
+6x
2
+3x
3
+6x
4
+9x
5
+x
8
=1440
xj≥0 j=1,5 xj≥0 j=1,8
Сб
Б
Ао
16
10
16
14
12
0
0
0
x
1
x
2
x
3
x
4
x
5
x
6
x
7
x
8
0
x
6
1080
6
3
3
3
3
1
0
0
0
x
7
840
4
2
6
2
2
0
1
0
0
x
8
1440
6
6
3
6
9
0
0
1
∆j
z=0
-16
-10
-16
-14
-12
0
0
0
16
x
1
180
1
1/2
1/2
1/2
1/2
1/6
0
0
0
x
7
120
0
0
4
2
0
-2/3
1
0
0
x
8
360
0
3
0
3
6
-1
0
1
∆j
z=2880
0
-2
-8
-6
-4
2 ⅔
0
0
16
x
1
165
1
½
0
¼
½
¼
-1/8
0
16
x
3
30
0
0
1
½
0
-1/6
¼
0
0
x
8
360
0
3
0
3
6
-1
0
1
∆j
z=3120
0
-2
0
-2
-4
1 ⅓
2
0
16
x
1
135
1
¼
0
0
0
1/3
-1/8
-1/12
16
x
3
30
0
0
1
½
0
-1/6
¼
0
12
x
5
60
0
½
0
½
1
-1/6
0
1/6
∆j
z=3360
0
0
0
0
0
2/3
2
2/3
16
x
1
105
1
0
0
-1/4
-1/2
5/12
-1/8
-1/6
16
x
3
30
0
0
1
1/2
0
-1/6
¼
0
10
x
2
120
0
1
0
1
2
-1/3
0
1/3
∆j
z=3360
0
0
0
0
0
2/3
2
2/3
16
x
1
135
1
¼
0
0
0
1/3
-1/8
-1/12
14
x
4
60
0
0
2
1
0
-1/3
½
0
12
x
5
30
0
½
-1
0
1
0
-1/4
1/6
∆j
z=3360
0
0
0
0
0
2/3
2
2/3
16
x
1
120
1
0
½
0
-1/2
1/3
0
-1/6
14
x
4
60
0
0
2
1
0
-1/3
½
0
10
x
2
60
0
1
-2
0
2
0
-1/2
1/3
∆j
z=3360
0
0
0
0
0
2/3
2
2/3
max Z=3360 X
1
opt=(135;0;30;0;60)
X
2
opt=(105;120;30;0;0)
X
3
opt=(135;0;0;60;30)
X
4
opt=(120;60;0;60;0)

Задачата има четири оптимални плана. Поставено е условие да се намери такъв
план на производство, което включва всички видове продукти. За намирането
му ще използваме следната формула
:
X’ opt =λ
1
*X
1
opt+ λ
2
*X
2
opt+ λ
3
*X
3
opt+ λ
4
*X
4
opt , където λ
1
+ λ
2
+λ
3
+ λ
4
=1
За да намерим оптимално небазсино решение ще зададем произволни
стойности на параметрите λ
λ
1
=0,55 ; λ
2
=0,10; λ
3
=0,25; λ
4
=0,10
x
1
=0,55.135 + 0,10.105+ 0,25.135+ 0,10.120=130,5
x
2
=0,55.0 + 0,10.120+ 0,25.0+ 0,10.60=18
x
3
=0,55.30 + 0,10.30+ 0,25.0+ 0,10.0=19,5
x
4
=0,55.0 + 0,10.0+ 0,25.60+ 0,10.60=21
x
5
=0,55.60 + 0,10.0+ 0,25.30+ 0,10.0=40,5
Оптималния небазисен план е :
X’ opt= (130,5; 18; 19,5; 21; 40,5)
Намерения оптимален план удовлетворява условието сбора от четирите вида
продукция да не е по-голям от обема на първи вид продуция.
Видове ресурси
Разходни норми за едница продукция
Налични
ресурси
I
II
III
IV
A
6
3
3
3
1080
B
4
2
6
4
840
C
6
6
3
6
1440
Печалба
16
6
12
4
c
j
max: Z =16x
1
+6x
2
+12x
3
+4x
4
max: Z=16x
1
+6x
2
+12x
3
+4x
4
+0x
5
+0x
6
+0x
7
6x
1
+3x
2
+3x
3
+3x
4
≤1080 6x
1
+3x
2
+3x
3
+3x
4
+x
5
=1080
4x
1
+2x
2
+6x
3
+4x
4
≤8480 4x
1
+2x
2
+6x
3
+4x
4
+x
6
=840
6x
1
+6x
2
+3x
3
+6x
4
≤1440 6x
1
+6x
2
+3x
3
+6x
4
+x
7
=1440
xj≥0 j=1,4 xj≥0 j=1,7

Сб
Б
Ао
16
6
12
4
0
0
0
x
1
x
2
x
3
x
4
x
5
x
6
x
7
0
x
5
1080
6
3
3
3
1
0
0
0
x
6
840
4
2
6
4
0
1
0
0
x
7
1440
6
6
3
6
0
0
1
∆j
z=0
-16
-6
-12
-4
0
0
0
16
x
1
180
1
1/2
½
½
1/6
0
0
0
x
6
120
0
0
4
2
-2/3
1
0
0
x
7
360
0
3
0
3
-1
0
1
∆j
z=2880
0
2
-4
4
2⅔
0
0
16
x
1
165
1
½
0
¼
¼
-1/8
0
12
x
3
30
0
0
1
½
-1/6
¼
0
0
x
7
360
0
3
0
3
-1
0
1
∆j
z=3000
0
2
0
6
2
1
0
max: Z=3000 Xopt=(165;0;30;0)
Решение:
Решената чрез симплекс метод задача е в основата на след оптималния
анализ, който от своя страна има за цел получаване на ценна информация
относно земането на уплравленско решение.
Решаването на задачата преминава през следната последователност:
1) Съставяне на математически модел на задачата, който исползва
следния теоретияен модел
:
max Z
=
при условия
≤ b
i
(i=1,m)
xj≥ 0 (j=1,n)
Моделът на поставената задача изглежда по следния начин
Асортимент на стоките
Това е определена съвкупност от стоки обединени от общ признак. Различаваме промишлен, вкл. номенклатурата на стоките, произведени от даден отрасъл като цяло или от отделни производствени предприятия...Асортимент на стоките
| Предмет: | Стокознание, Икономика |
| Тип: | Пищови |
| Брой страници: | 2 |
| Брой думи: | 512 |
| Брой символи: | 3795 |